Rules to make integration and differentiation easy
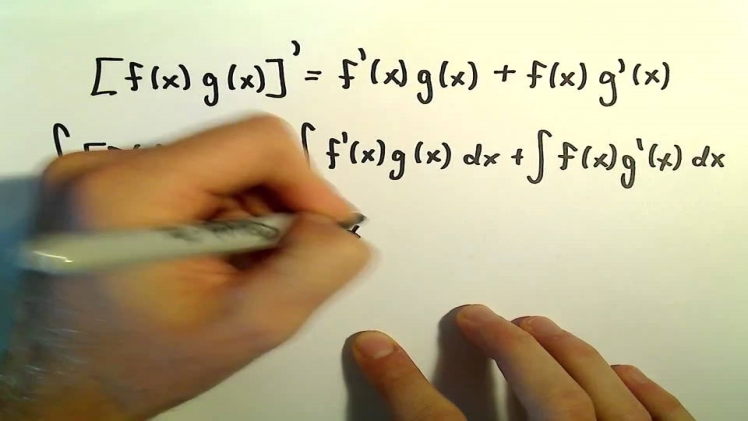
Calculus is a field of mathematics that is taught to students in their senior years of high school. Calculus is a branch of mathematics that is both ancient and widely utilized. It appears tough and complex to the students, but it can be readily grasped with frequent practice and hard commitment. It is regarded as one of the fields of mathematics that deals with continuous change.
buy Pepcid generic rxbuyonlinewithoutprescriptionrx.net over the counter
Calculus has a wide range of applications. It is used to calculate the area and volume of various bodies. Calculus also aids in determining the body’s center of mass.
Differentiation and integration are two topics that we cover in calculus. Differentiation and integration are carried out using some formula and using specific rules like product rule, chain rule, division rule. This article discusses mainly two types of rules: chain rule and product rule. First of all, let’s discuss what differentiation is. It can be defined as the rate of change of a function concerning other functions.
Differentiation is the process of breaking down a function into its constituent elements, while integration is the process of putting those pieces back together to generate the original function. In daily mathematics, both integration and differentiation have a wide range of applications. Let’s discuss the first rule which is applicable in both integrations as well as differentiation.
Chain rule
It is one among those rules which apply to the composite type of function. This rule helps in finding out the instantaneous rate of change between two functions.
Here are some steps which describe how chain rule is carried out:
- Determine whether or not The Chain Rule can be used. This is possible when the function is a composite function, which means that one function is nested over the other.
- After that, one must look at both the inner and outward functions.
- The most crucial step is to get the derivative of the outer function while ignoring the inner function.
buy isotretinoin generic noprescriptionrxbuyonline.com/isotretinoin.html over the counter
- Once the outer function’s derivative has been determined, the inner function’s derivative must be subtracted.
- Multiply the results from steps 4 and 5 to get the final result.
- The final step is to simplify the chain rule’s derivative.
- The chain rule is applied to many problems of physics, mathematics too.
Product rule
In mathematics, the product rule is a rule that can be used to compute the derivatives of two or more functions. In basic terms, the product rule allows us to quickly determine the derivative of two differentiable functions that are multiplied together by combining our knowledge of the power rule and the addition and subtraction rules for derivatives.
Product formulas can be easily applied with practice and one needs to know when he needs to use the rule. Practice is the key in mathematics, if one practices questions daily then he can easily excel in the subject.
Here are some of the basic applications of the product formula:
- It is used to solve trigonometric functions by reducing the number of steps to a minimum.
- This rule can also be used to calculate the rate of change in real-time.
- Product rules can also be used to solve many functions at once.
This article discusses everything regarding the product and chain rule. It gives all the application of both the rules. These rules are very necessary to get through to excel in two pillars of mathematics that are, differentiation and integration.
If one wants to know more about mathematics or computer coding, you can visit the website of Cuemath. Cuemath is a great initiative that is helping a lot of students to achieve their path to success. This website is helping students prepare for many competitive examinations too.





